10. Search in Rotated Sorted Array

There is an integer array nums sorted in ascending order (with distinct values).

Prior to being passed to your function, nums is possibly rotated at an unknown pivot index k (1 <= k < nums.length) such that the resulting array is [nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]] (0-indexed). For example, [0,1,2,4,5,6,7] might be rotated at pivot index 3 and become [4,5,6,7,0,1,2].

Given the array nums after the possible rotation and an integer target, return *the index of target if it is in nums, or -1 if it is not in *nums.

You must write an algorithm with O(log n) runtime complexity.

Example 1:

Input: nums = [4,5,6,7,0,1,2], target = 0
Output: 4

Example 2:

Input: nums = [4,5,6,7,0,1,2], target = 3
Output: -1

Example 3:

Input: nums = [1], target = 0
Output: -1

Constraints:

1 <= nums.length <= 5000
-104 <= nums[i] <= 104
All values of nums are unique.
nums is an ascending array that is possibly rotated.
-104 <= target <= 104

Solution

Overview

Define the pivot index as representing the smallest element in nums.

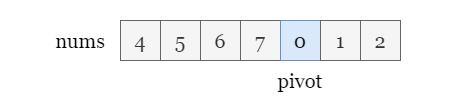
In a rotated sorted array, the pivot value signifies where the rotation occurs. It partitions the array (of length n) into two sorted portions nums[0 ~ pivot - 1] and nums[pivot ~ n - 1].

Approach 1: Find Pivot Index + Binary Search

Intuition

If you are not familiar with binary search, please refer to our explore cards Binary Search Explore Card. We will focus on the usage in this article and not the underlying principles or implementation details.

To pinpoint the pivot value, we can employ a modified binary search algorithm and find the leftmost element that is smaller than or equal to the last element in nums.

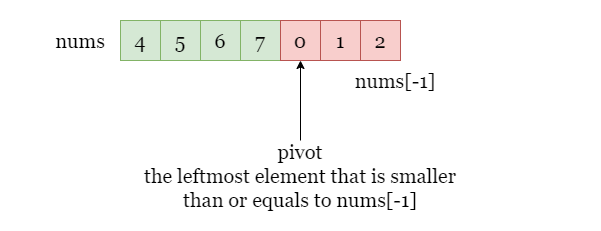
After identifying the middle element in the searching space [left ~ right], we compare nums[mid] with nums[-1].

If nums[mid] > nums[-1], it suggests that the pivot value lies on the right of nums[mid]. We will then proceed with the right half of the search space, which is [mid + 1 ~ right].
Otherwise, the pivot value is nums[mid] or it's situated to the left of nums[mid], we continue with the left half of the searching space, which is [left ~ mid - 1].

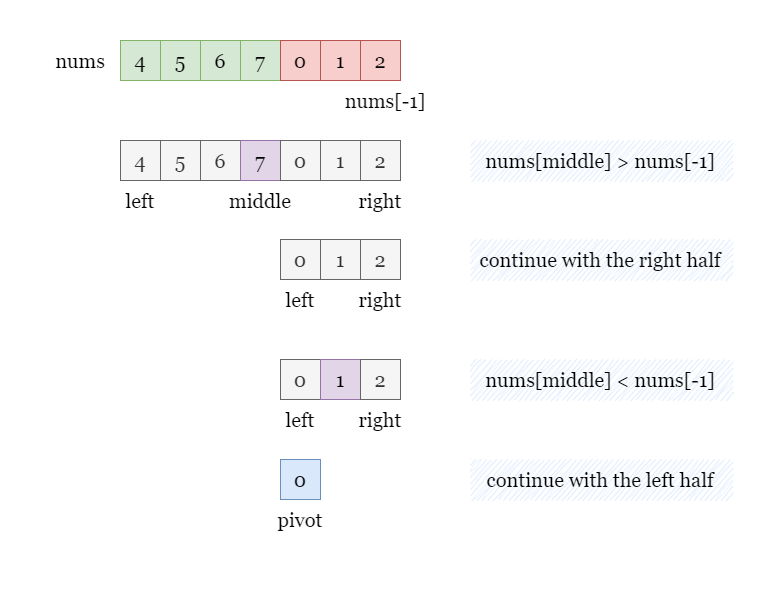
By determining the pivot value, we set the boundaries for our subsequent binary searches. Once we have the pivot value, we can execute two binary searches on each half of the array to locate the target element.

Note: the typical way to calculate mid is (left + right) / 2. However, a safer way is left + (right - left) / 2. The two equations are equivalent, but the second one is safer because it guarantees no number larger than right is ever stored. In the first equation, if left + right is huge, then it could end up overflowing.

Algorithm

Perform a binary search to locate the pivot element by initializing the boundaries of the searching space as left = 0 and right = n - 1. While left < right:
- Let mid = left + (right - left) // 2.
- If nums[mid] > nums[n - 1], this suggests that pivot is located to the right of mid, hence we set left = mid + 1. Otherwise, pivot could be either at mid or to the left of mid, in which case we should set right = mid - 1.
Upon completion of the binary search, we have the pivot index denoted as pivot = left.
nums consists of two sorted subarrays, nums[0 ~ left - 1] and nums[left ~ n - 1].
Perform a binary search over nums[0 ~ left - 1] for target. If target is within this subarray, return its index.
Otherwise, perform a binary search over nums[left ~ n - 1] for target. If target is within this subarray, return its index. Otherwise, return -1.

Implementation

JavaScript
C++

var search = function (nums, target) {
    let n = nums.length;
    let left = 0,
        right = n - 1;
    // Find the index of the pivot element (the smallest element)
    while (left <= right) {
        let mid = Math.floor((left + right) / 2);
        if (nums[mid] > nums[n - 1]) {
            left = mid + 1;
        } else {
            right = mid - 1;
        }
    }
    function binarySearch(left_boundary, right_boundary, target) {
        let left = left_boundary,
            right = right_boundary;
        while (left <= right) {
            let mid = Math.floor((left + right) / 2);
            if (nums[mid] == target) {
                return mid;
            } else if (nums[mid] > target) {
                right = mid - 1;
            } else {
                left = mid + 1;
            }
        }
        return -1;
    }
    // Binary search over elements on the pivot element's left
    let answer = binarySearch(0, left - 1, target);
    if (answer != -1) {
        return answer;
    }
    // Binary search over elements on the pivot element's right
    return binarySearch(left, n - 1, target);
};

class Solution {
public:
    int search(vector<int>& nums, int target) {
        int n = nums.size();
        int left = 0, right = n - 1;
        // Find the index of the pivot element (the smallest element)
        while (left <= right) {
            int mid = (left + right) / 2;
            if (nums[mid] > nums[n - 1]) {
                left = mid + 1;
            } else {
                right = mid - 1;
            }
        }
        // Binary search over elements on the pivot element's left
        int answer = binarySearch(nums, 0, left - 1, target);
        if (answer != -1) {
            return answer;
        }
        // Binary search over elements on the pivot element's right
        return binarySearch(nums, left, n - 1, target);
    }
    // Binary search over an inclusive range [left_boundary ~ right_boundary]
    int binarySearch(vector<int>& nums, int leftBoundary, int rightBoundary,
                     int target) {
        int left = leftBoundary, right = rightBoundary;
        while (left <= right) {
            int mid = (left + right) / 2;
            if (nums[mid] == target) {
                return mid;
            } else if (nums[mid] > target) {
                right = mid - 1;
            } else {
                left = mid + 1;
            }
        }
        return -1;
    }
};

Complexity Analysis

Let n be the length of nums.

Time complexity: O(logn)
- The algorithm requires one binary search to locate pivot, and at most 2 binary searches to find target. Each binary search takes O(logn) time.
Space complexity: O(1)
- We only need to update several parameters left, right and mid, which takes O(1) space.

Approach 2: Find Pivot Index + Binary Search with Shift

Intuition

The array we're working with has been rotated by a certain number of steps, which means we can't apply a regular binary search to the modified array. However, if we can revert this array to its original sorted form, then a conventional binary search becomes a viable approach.

Our key task is to locate pivot, the index of the smallest value in nums. Notably, nums[pivot] would have been at index 0 in the unrotated, original array. Hence, if we were to rotate it to the right by n - pivot steps (taking the modulus of n into account), it would return to its original position, index 0.

Applying the same transformation to every element enables us to revert the rotated array back to its original, sorted form.

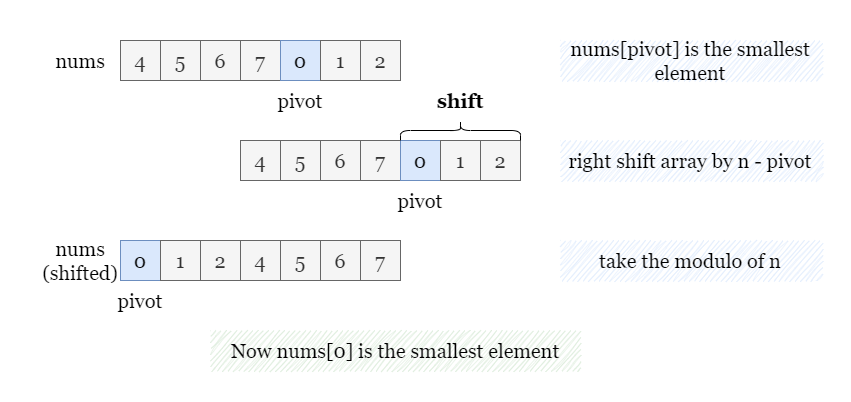
At this point, we can perform a conventional binary search to locate the target. Let's assume that nums[i] = target. Remembering that we had to shift every element to the right by n - pivot steps to reach the sorted version of nums, we now need to shift the index in the sorted nums to the left by n - pivot steps to find its corresponding index, i, in the original nums. This gives us i - (n - pivot) (taking the modulus of n into account).

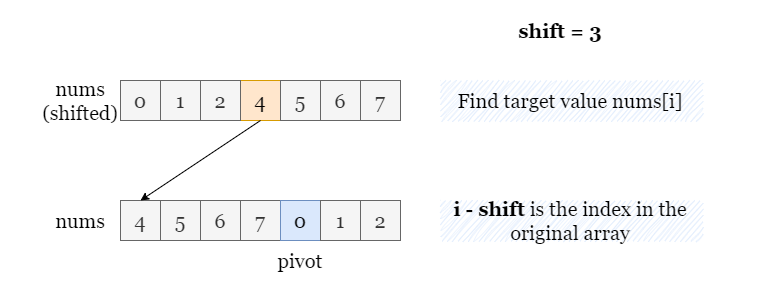
Crucially, there's no need to actually create the sorted version of nums from the original nums. We can simply represent the sorted nums by shifting the indices.

Algorithm

Perform a binary search to locate the pivot element by initializing the boundaries of the searching space as left = 0 and right = n - 1. While left < right:
- Let mid = left + (right - left) // 2.
- If nums[mid] > nums[n - 1], this suggests that pivot is located to the right of mid, hence we set left = mid + 1. Otherwise, pivot could be either at mid or to the left of mid, in which case we should set right = mid - 1.
Upon completion of the binary search, we have the pivot index denoted as pivot = left.
Set the boundaries of the search space as (pivot + shift) % n and (pivot - 1 + shift) % n.
While left < right, we get the middle index mid = (left + right) // 2, and compare nums[(mid - shift + n) % n] with target.
- If nums[(mid - shift + n) % n] is equal to target, return mid - shift + n
- If nums[(mid - shift + n) % n] > target, continue with the left half by setting right as mid - 1.
- If nums[(mid - shift + n) % n] < target, continue with the right half by setting left as mid + 1.
Return -1 once the binary search is complete.

Implementation

Solution:

JavaScript
C++

var search = function (nums, target) {
    var n = nums.length;
    var left = 0,
        right = n - 1;
    // Find the index of the pivot element (the smallest element)
    while (left <= right) {
        var mid = Math.floor((left + right) / 2);
        if (nums[mid] > nums[n - 1]) {
            left = mid + 1;
        } else {
            right = mid - 1;
        }
    }
    return shiftedBinarySearch(nums, left, target);
    // Shift elements in a circular manner, with the pivot element at index 0.
    // Then perform a regular binary search
    function shiftedBinarySearch(nums, pivot, target) {
        var n = nums.length;
        var shift = n - pivot;
        var left = (pivot + shift) % n;
        var right = (pivot - 1 + shift) % n;
        while (left <= right) {
            var mid = Math.floor((left + right) / 2);
            if (nums[(mid - shift + n) % n] == target) {
                return (mid - shift + n) % n;
            } else if (nums[(mid - shift + n) % n] > target) {
                right = mid - 1;
            } else {
                left = mid + 1;
            }
        }
        return -1;
    }
};

class Solution {
public:
    int search(vector<int>& nums, int target) {
        int n = nums.size();
        int left = 0, right = n - 1;
        // Find the index of the pivot element (the smallest element)
        while (left <= right) {
            int mid = (left + right) / 2;
            if (nums[mid] > nums[n - 1]) {
                left = mid + 1;
            } else {
                right = mid - 1;
            }
        }
        return shiftedBinarySearch(nums, left, target);
    }
    // Shift elements in a circular manner, with the pivot element at index 0.
    // Then perform a regular binary search
    int shiftedBinarySearch(vector<int>& nums, int pivot, int target) {
        int n = nums.size();
        int shift = n - pivot;
        int left = (pivot + shift) % n;
        int right = (pivot - 1 + shift) % n;
        while (left <= right) {
            int mid = (left + right) / 2;
            if (nums[(mid - shift + n) % n] == target) {
                return (mid - shift + n) % n;
            } else if (nums[(mid - shift + n) % n] > target) {
                right = mid - 1;
            } else {
                left = mid + 1;
            }
        }
        return -1;
    }
};

Complexity Analysis

Let n be the length of nums.

Time complexity: O(logn)
- The algorithm requires one binary search to locate pivot and one binary search over the shifted indices to find target. Each binary search takes O(logn) time.
Space complexity: O(1)
- We only need to update several parameters left, right mid and shift, which takes O(1) space.

Approach 3: One Binary Search

Intuition

The two preceding approaches both comprise two steps:

Perform a binary search to identify the pivot index.
Conduct another binary search to locate the target value.

However, we can perform these two steps within a single binary search.

Let's take a step back and consider a regular binary search. Why are we able to confidently discard half of the array after comparing target with the middle value nums[mid]? The reason is that both halves of the array are sorted. Hence, if target is less than the middle value, it's assured to be smaller than every value in the right half. If target is larger than the middle value, it's guaranteed to be larger than every value in the left half. Therefore, we can safely discard one half of nums in either case.

However, a rotated sorted array may not possess this characteristic -- we can't determine whether target is definitively not in the array just by comparing boundary values.

If we cut a subarray nums[left ~ right] by the index mid. We split this subarray into 3 parts:

subarray nums[left ~ mid - 1]
element nums[mid].
subarray nums[mid + 1, right].

It is important to note that there is at most one rotated sorted array in the two subarrays, which means that there is at least one sorted array for comparison.

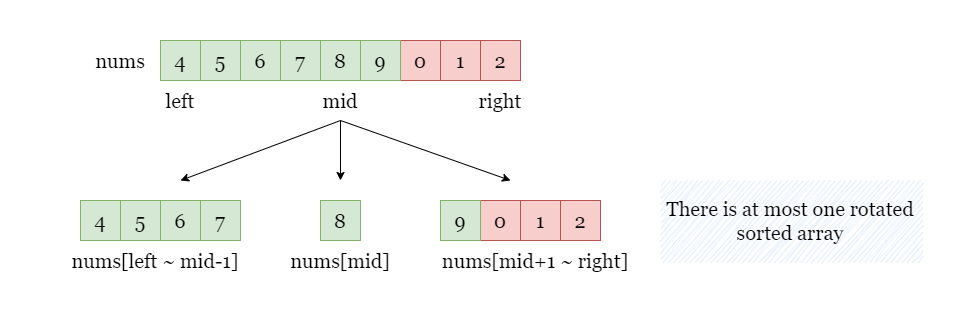
Therefore, we can compare target with the sorted half to decide which subarray to retain for the next round.

It is straightforward to determine if a sorted array A[l ~ r] could possibly contain target, we can simply compare target with two boundary values A[l] and A[r].

If A[l] <= target <= A[r], then A[l ~ r] might contain target, which needs to be verified by binary search, we will continue with this subarray.

Otherwise, target is guaranteed to not be in A[l ~ r], and there is no need to search over this array, we will continue with the other subarray.

To sum up, there are 3 possible cases after comparing target with nums[mid]:

Case 1. If nums[mid] = target, which denotes that we have found target, return mid as its index.

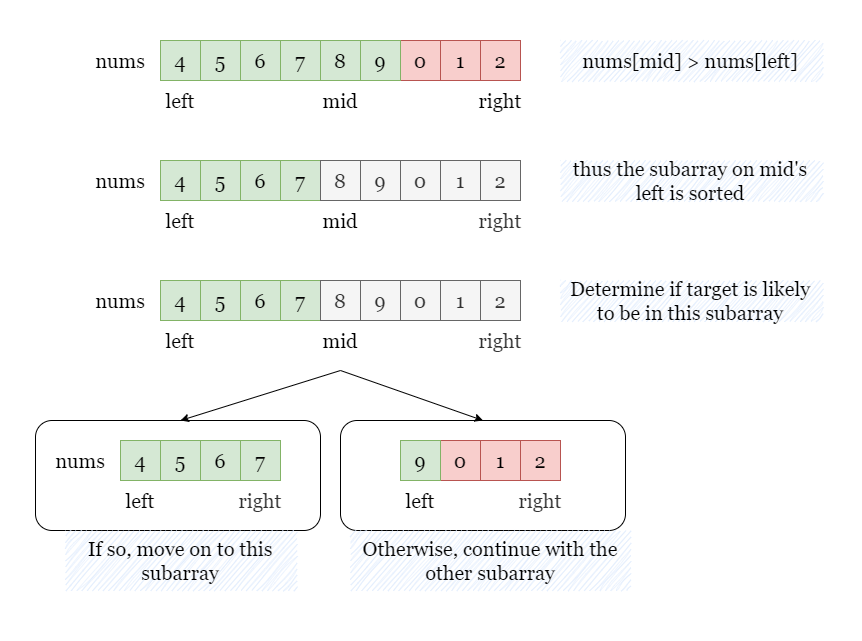
Case 2. If nums[mid] >= nums[left]. It implies that the left subarray nums[left ~ mid] is sorted. We can determine whether to proceed with this subarray by comparing target with the boundary elements:

If nums[left] <= target and target < nums[mid], it suggests that the sorted left half might include target while the other half does not contain target. Consequently, we focus on the left half for further steps.
Otherwise, the left half is guaranteed not to contain target, and we will move on to the right half.

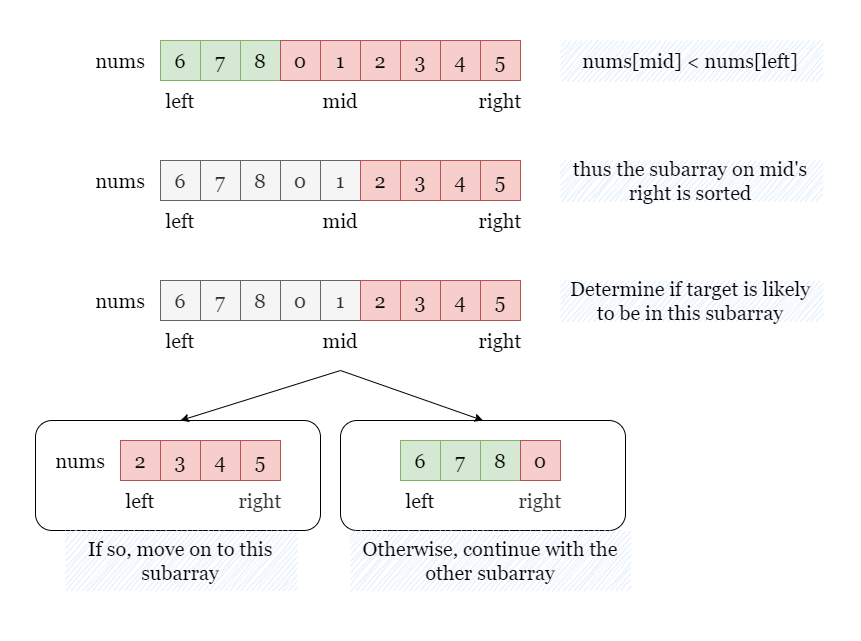
Case 3. If nums[mid] < nums[left], it implies that the left subarray is rotated and the right subarray nums[mid ~ right] is sorted. Therefore, we can determine whether to proceed with the right subarray by comparing the target with its boundary elements:

If nums[mid] < target and target < nums[right], it implies that the sorted right half might contain target. As a result, we will move on with the right half.
Otherwise, the right half is guaranteed not to contain target, and we will move on to the left half.

Algorithm

Initialize pointers:
- Set left to 0.
- Set right to n - 1 where n is the length of the array nums.
Perform binary search:
- While left is less than or equal to right:
  - Calculate the middle index mid as left + (right - left) / 2.
  - Case 1: Check if the middle element nums[mid] is equal to target.
    - If true, return mid as the index of target.
  - Case 2: Check if the subarray from left to mid is sorted (nums[mid] >= nums[left]).
    - If target is within the range [nums[left], nums[mid]):
      - Adjust the search range by setting right to mid - 1.
    - Otherwise:
      - Adjust the search range by setting left to mid + 1.
  - Case 3: If the subarray from mid to right is sorted (nums[mid] > nums[right]):
    - If target is within the range (nums[mid], nums[right]]:
      - Adjust the search range by setting left to mid + 1.
    - Otherwise:
      - Adjust the search range by setting right to mid - 1.
If the target is not found, return -1.

Implementation

JavaScript
C++

var search = function (nums, target) {
    let n = nums.length;
    let left = 0,
        right = n - 1;
    while (left <= right) {
        let mid = left + (((right - left) / 2) | 0);
        // Case 1: find target
        if (nums[mid] == target) return mid;
        // Case 2: Subarray on mid's left is sorted
        else if (nums[mid] >= nums[left]) {
            if (target >= nums[left] && target < nums[mid]) right = mid - 1;
            else left = mid + 1;
        }
        // Case 3: Subarray on mid's right is sorted
        else {
            if (target <= nums[right] && target > nums[mid]) left = mid + 1;
            else right = mid - 1;
        }
    }
    return -1;
};

class Solution {
public:
    int search(vector<int>& nums, int target) {
        int n = nums.size();
        int left = 0, right = n - 1;
        while (left <= right) {
            int mid = left + (right - left) / 2;
            // Case 1: Find target
            if (nums[mid] == target) {
                return mid;
            }
            // Case 2: Subarray on mid's left is sorted
            else if (nums[mid] >= nums[left]) {
                if (target >= nums[left] && target < nums[mid]) {
                    right = mid - 1;
                } else {
                    left = mid + 1;
                }
            }
            // Case 3: Subarray on mid's right is sorted
            else {
                if (target <= nums[right] && target > nums[mid]) {
                    left = mid + 1;
                } else {
                    right = mid - 1;
                }
            }
        }
        return -1;
    }
};

Complexity Analysis

Let n be the length of nums.

Time complexity: O(logn)
- This algorithm only requires one binary search over nums.
Space complexity: O(1)
- We only need to update several parameters left, right and mid, which takes O(1) space.

10. Search in Rotated Sorted Array

Example 1:​

Example 2:​

Example 3:​

Constraints:​

Solution​

Overview​

Approach 1: Find Pivot Index + Binary Search​

Intuition​

Algorithm​

Implementation​

Complexity Analysis​

Approach 2: Find Pivot Index + Binary Search with Shift​

Intuition​

Algorithm​

Implementation​

Solution:​

Complexity Analysis​

Approach 3: One Binary Search​

Intuition​

Algorithm​

Implementation​

Complexity Analysis​

Example 1:

Example 2:

Example 3:

Constraints:

Solution

Overview

Approach 1: Find Pivot Index + Binary Search

Intuition

Algorithm

Implementation

Complexity Analysis

Approach 2: Find Pivot Index + Binary Search with Shift

Intuition

Algorithm

Implementation

Solution:

Complexity Analysis

Approach 3: One Binary Search

Intuition

Algorithm

Implementation

Complexity Analysis