8. Merge Two Sorted Lists

LC21

You are given the heads of two sorted linked lists list1 and list2.

Merge the two lists into one sorted list. The list should be made by splicing together the nodes of the first two lists.

Return the head of the merged linked list.

Example 1:

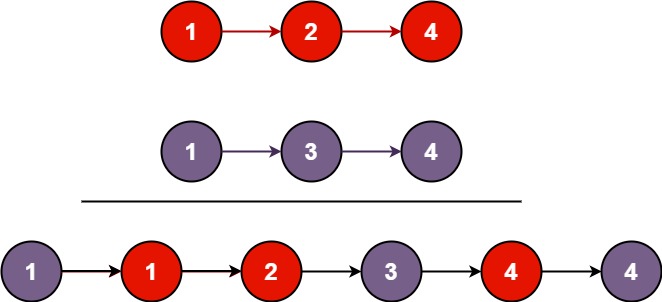
Input: list1 = [1,2,4], list2 = [1,3,4]
Output: [1,1,2,3,4,4]

Example 2:

Input: list1 = [], list2 = []
Output: []

Example 3:

Input: list1 = [], list2 = [0]
Output: [0]

Constraints:

• The number of nodes in both lists is in the range [0, 50].
• -100 <= Node.val <= 100
• Both list1 and list2 are sorted in non-decreasing order.

Solution Article

Approach 1: Recursion

Intuition

We can recursively define the result of a merge operation on two lists as
the following (avoiding the corner case logic surrounding empty lists):

{list1[0]+merge(list1[1:],list2)list2[0]+merge(list1,list2[1:])​list1[0]<list2[0]otherwise​

Namely, the smaller of the two lists' heads plus the result of a merge on
the rest of the elements.

Algorithm

We model the above recurrence directly, first accounting for edge cases.
Specifically, if either of l1 or l2 is initially null, there is no
merge to perform, so we simply return the non-null list. Otherwise, we
determine which of l1 and l2 has a smaller head, and recursively set the
next value for that head to the next merge result. Given that both lists
are null-terminated, the recursion will eventually terminate.

Solution:

JavaScript

function mergeTwoLists(l1, l2) {
    if (l1 === null) {
        return l2;
    } else if (l2 === null) {
        return l1;
    } else if (l1.val < l2.val) {
        l1.next = mergeTwoLists(l1.next, l2);
        return l1;
    } else {
        l2.next = mergeTwoLists(l1, l2.next);
        return l2;
    }
}

C++

class Solution {
public:
    ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {
        if (l1 == nullptr) {
            return l2;
        } else if (l2 == nullptr) {
            return l1;
        } else if (l1->val < l2->val) {
            l1->next = mergeTwoLists(l1->next, l2);
            return l1;
        } else {
            l2->next = mergeTwoLists(l1, l2->next);
            return l2;
        }
    }
};

Complexity Analysis

• Time complexity : O(n+m)

  Because each recursive call increments the pointer to l1 or l2 by one (approaching the dangling null at the end of each list), there will be exactly one call to mergeTwoLists per element in each list. Therefore, the time complexity is linear in the combined size of the lists.

• Space complexity : O(n+m)

  The first call to mergeTwoLists does not return until the ends of both l1 and l2 have been reached, so n+m stack frames consume O(n+m) space.

---

Approach 2: Iteration

Intuition

We can achieve the same idea via iteration by assuming that l1 is entirely
less than l2 and processing the elements one-by-one, inserting elements of
l2 in the necessary places in l1.

Algorithm

First, we set up a false "prehead" node that allows us to easily return the
head of the merged list later. We also maintain a prev pointer, which
points to the current node for which we are considering adjusting its next
pointer. Then, we do the following until at least one of l1 and l2 points
to null: if the value at l1 is less than or equal to the value at l2,
then we connect l1 to the previous node and increment l1. Otherwise, we
do the same, but for l2. Then, regardless of which list we connected, we
increment prev to keep it one step behind one of our list heads.

After the loop terminates, at most one of l1 and l2 is non-null.
Therefore (because the input lists were in sorted order), if either list is
non-null, it contains only elements greater than all of the
previously-merged elements. This means that we can simply connect the
non-null list to the merged list and return it.

Solution:

JavaScript

function mergeTwoLists(l1, l2) {
    let prehead = new ListNode(-1);
    let prev = prehead;
    while (l1 != null && l2 != null) {
        if (l1.val <= l2.val) {
            prev.next = l1;
            l1 = l1.next;
        } else {
            prev.next = l2;
            l2 = l2.next;
        }
        prev = prev.next;
    }
    if (l1 != null) {
        prev.next = l1;
    } else {
        prev.next = l2;
    }
    return prehead.next;
}

C++

class Solution {
public:
    ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {
        // maintain an unchanging reference to node ahead of the return node.
        ListNode prehead(-1);
        ListNode* prev = &prehead;
        while (l1 != nullptr && l2 != nullptr) {
            if (l1->val <= l2->val) {
                prev->next = l1;
                l1 = l1->next;
            } else {
                prev->next = l2;
                l2 = l2->next;
            }
            prev = prev->next;
        }
        // At least one of l1 and l2 can still have nodes at this point, so
        // connect the non-null list to the end of the merged list.
        prev->next = l1 == nullptr ? l2 : l1;
        return prehead.next;
    }
};

Complexity Analysis

• Time complexity : O(n+m)

  Because exactly one of l1 and l2 is incremented on each loop
  iteration, the while loop runs for a number of iterations equal to the
  sum of the lengths of the two lists. All other work is constant, so the
  overall complexity is linear.

• Space complexity : O(1)

  The iterative approach only allocates a few pointers, so it has a
  constant overall memory footprint