Skip to main content

9. Merge k Sorted Lists

LC23

You are given an array of k linked-lists lists, each linked-list is sorted in ascending order.

Merge all the linked-lists into one sorted linked-list and return it.

Example 1:​

Input: lists = [[1,4,5],[1,3,4],[2,6]]
Output: [1,1,2,3,4,4,5,6]
Explanation: The linked-lists are:
[
  1->4->5,
  1->3->4,
  2->6
]
merging them into one sorted list:
1->1->2->3->4->4->5->6

Example 2:​

Input: lists = []
Output: []

Example 3:​

Input: lists = [[]]
Output: []

Constraints:​

  • k == lists.length
  • 0 <= k <= 104
  • 0 <= lists[i].length <= 500
  • -104 <= lists[i][j] <= 104
  • lists[i] is sorted in ascending order.
  • The sum of lists[i].length will not exceed 104.

Solution Article​

Approach 1: Brute Force​

Intuition & Algorithm​

  • Traverse all the linked lists and collect the values of the nodes into an array.
  • Sort and iterate over this array to get the proper value of nodes.
  • Create a new sorted linked list and extend it with the new nodes.

As for sorting, you can refer here for more about sorting algorithms.

Solution:​

function mergeKLists(lists) {
    let nodes = [];
    let dummy = new ListNode(0);
    let point = dummy;
    lists.forEach((l) => {
        while (l) {
            nodes.push(l.val);
            l = l.next;
        }
    });
    nodes
        .sort((a, b) => a - b)
        .forEach((n) => {
            point.next = new ListNode(n);
            point = point.next;
        });
    return dummy.next;
}

Complexity Analysis​

  • Time complexity : O(NlogN) where N is the total number of nodes.

    • Collecting all the values costs O(N) time.
    • A stable sorting algorithm costs O(NlogN) time.
    • Iterating for creating the linked list costs O(N) time.

  • Space complexity : O(N).

    • Sorting cost O(N) space (depends on the algorithm you choose).
    • Creating a new linked list costs O(N) space.

Approach 2: Compare one by one​

Algorithm​

  • Compare every k nodes (head of every linked list) and get the node with the smallest value.
  • Extend the final sorted linked list with the selected nodes.

Complexity Analysis​

  • Time complexity : O(kN) where k is the number of linked lists.

    • Almost every selection of node in final linked costs O(k) (k-1 times comparison).
    • There are N nodes in the final linked list.

  • Space complexity :

    • O(n) Creating a new linked list costs O(n) space.
    • O(1) It's not hard to apply in-place method - connect selected nodes instead of creating new nodes to fill the new linked list.

Approach 3: Optimize Approach 2 by Priority Queue​

Algorithm​

Almost the same as the one above but optimize the comparison process by priority queue. You can refer here for more information about it.

Solution:​

var mergeKLists = function (lists) {
    const compareNodes = (l1, l2) => {
        if (l1.val > l2.val) return 1;
        if (l1.val < l2.val) return -1;
        return 0;
    };

    const pq = new PriorityQueue({ compare: compareNodes });

    lists.forEach((l) => {
        if (l != null) {
            pq.enqueue(l);
        }
    });

    let head = new ListNode(0); // Assume ListNode is defined
    let point = head;

    while (!pq.isEmpty()) {
        point.next = pq.dequeue();
        point = point.next;
        if (point.next != null) {
            pq.enqueue(point.next);
        }
    }

    return head.next;
};

Complexity Analysis​

  • Time complexity : O(Nlogk) where k is the number of linked lists.

    • The comparison cost will be reduced to O(logk) for every pop and insertion to priority queue. But finding the node with the smallest value just costs O(1) time.
    • There are N nodes in the final linked list.

  • Space complexity :

    • O(n) Creating a new linked list costs O(n) space.
    • O(k) The code above present applies in-place method which cost O(1) space. And the priority queue (often implemented with heaps) costs O(k) space (it's far less than N in most situations).

Approach 4: Merge lists one by one​

Algorithm​

Convert merge k lists problem to merge 2 lists (k-1) times. Here is the merge 2 lists problem page.

Complexity Analysis​

  • Time complexity : O(kN) where k is the number of linked lists.

    • We can merge two sorted linked list in O(n) time where n is the total number of nodes in two lists.
    • Sum up the merge process and we can get: O(∑i=1k-1​(i∗(kN​)+kN​))=O(kN).

  • Space complexity : O(1)

    • We can merge two sorted linked list in O(1) space.

Approach 5: Merge with Divide And Conquer​

Intuition & Algorithm​

This approach walks alongside the one above but is improved a lot. We don't need to traverse most nodes many times repeatedly

  • Pair up k lists and merge each pair.

  • After the first pairing, k lists are merged into k/2 lists with average 2N/k length, then k/4, k/8 and so on.

  • Repeat this procedure until we get the final sorted linked list.

Thus, we'll traverse almost N nodes per pairing and merging, and repeat this procedure about log2​k times.

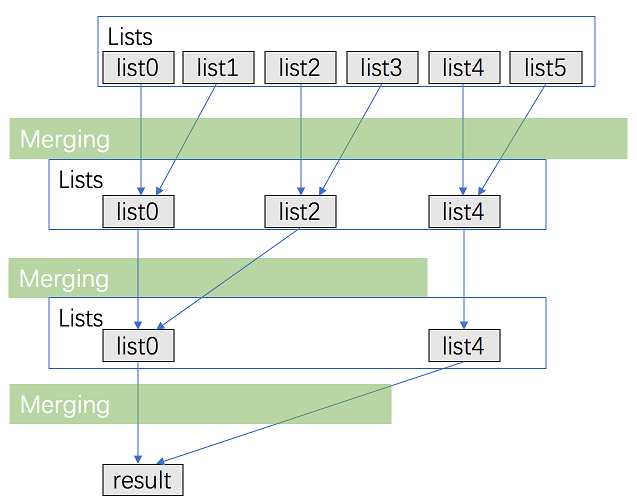
Solution:​

// Definition for singly-linked list.
// function ListNode(val, next) {
//     this.val = (val === undefined ? 0 : val)
//     this.next = (next === undefined ? null : next)
// }
function mergeKLists(lists) {
    var amount = lists.length;
    var interval = 1;
    while (interval < amount) {
        for (let i = 0; i < amount - interval; i += interval * 2) {
            lists[i] = merge2Lists(lists[i], lists[i + interval]);
        }
        interval *= 2;
    }
    return amount > 0 ? lists[0] : null;
}
function merge2Lists(l1, l2) {
    var head = new ListNode(0);
    var point = head;
    while (l1 && l2) {
        if (l1.val <= l2.val) {
            point.next = l1;
            l1 = l1.next;
        } else {
            point.next = l2;
            l2 = l1;
            l1 = point.next.next;
        }
        point = point.next;
    }
    if (!l1) {
        point.next = l2;
    } else {
        point.next = l1;
    }
    return head.next;
}

Complexity Analysis​

  • Time complexity : O(Nlogk) where k is the number of linked lists.

    • We can merge two sorted linked list in O(n) time where n is the total number of nodes in two lists.
    • Sum up the merge process and we can get: O(∑i=1log2​k​N)=O(Nlogk)

  • Space complexity : O(1)

    • We can merge two sorted linked lists in O(1) space.