4. Container With Most Water

LC11

You are given an integer array height of length n. There are n vertical lines drawn such that the two endpoints of the ith line are (i, 0) and (i, height[i]).

Find two lines that together with the x-axis form a container, such that the container contains the most water.

Return the maximum amount of water a container can store.

Notice that you may not slant the container.

Example 1:

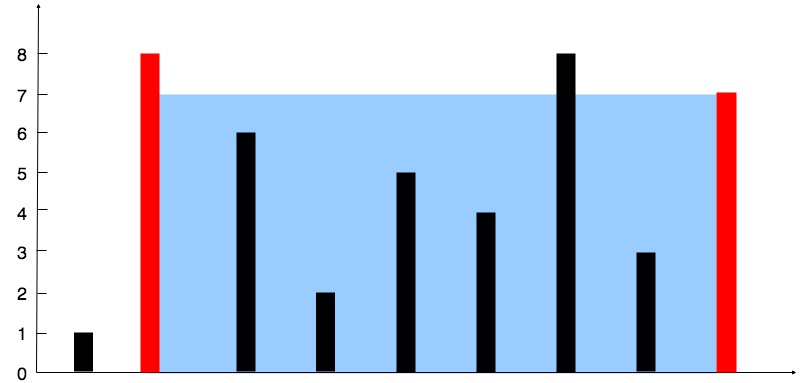
Input: height = [1,8,6,2,5,4,8,3,7] Output: 49 Explanation: The above vertical lines are represented by array [1,8,6,2,5,4,8,3,7]. In this case, the max area of water (blue section) the container can contain is 49.

Example 2:

Input: height = [1,1] Output: 1

Constraints:

• n == height.length
• 2 <= n <= 105
• 0 <= height[i] <= 104

Approach:

Two Pointer Approach

Algorithm

The intuition behind this approach is that the area formed between the lines will always be limited by the height of the shorter line. Further, the farther the lines, the more will be the area obtained.

We take two pointers, one at the beginning and one at the end of the array constituting the length of the lines. Further, we maintain a variable maxarea to store the maximum area obtained till now. At every step, we find out the area formed between them, update maxarea and move the pointer pointing to the shorter line towards the other end by one step.

Implementation

/**
 * @param {number[]} height
 * @return {number}
 */
var maxArea = function(height) {
  let left = 0;
  let right = height.length-1;
  let maxarea = 0;
  while(left<right) {
    let width = right - left;
    let area = height[left] < height[right] ? height[left]*(width) : height[right]*(width);
    maxarea = Math.max(maxarea, area);
    if (height[left] < height[right]) {
      left++;
    } else {
      right--;
    }
  }
  return maxarea;
};

const height = [1,8,6,2,5,4,8,3,7];
console.log(maxArea(height));

Complexity Analysis

• Time complexity: O(n). Single pass.

• Space complexity: O(1). Constant space is used.